TRAVEL TIME DECAY USING EXPONENTIAL AND LOGISTIC REGRESSION
Renissance Planning
January 6, 2020
1 INTRODUCTION
Many methods exist to estimate decay in value for trips with varying characteristics. Depending on the method, the characteristics considered can be expansive, including travel time, financial cost of the trip, purpose of the trip, and travel conditions, among others. One of the simplest forms of travel time decay modeling is a single-cost model, which assumes one characteristic to be the sole determinant of trip value. Most often, this single cost is taken to be trip duration. In this case, the modeled relationship is intuitive: longer trips have less value. This method is useful in that it is highly interpretable and mathematically noncomplex, providing an approachable and practical way to explore travel time decay.
This paper details the use of two forms of regression for single-cost travel time decay modeling with trip duration. It suggests exponential regression when trip value decays quickly at low time values, and logistic regression when trip value tends to stay high until larger time values. It also explores the use of generalized cost in this model formulation, which improves on a raw duration measure by aggregating all types of costs into a single measure.
2 DATA
The data comes from the Massachusetts Travel Survey (MTS), conducted by the Massachusetts Department of Transportation and published in June 2012. It was provided by the Metropolitan Area Planning Council (MAPC), which serves Boston, MA and its metropolitan region.
The data includes 190,215 trip records from 37,023 persons across 15,033 households in Massachusetts. Though the full dataset includes a multitude of variables, trip duration was only covariate of interest, because the ultimate models would include only this variable. However, mode and trip purpose were used to separate records for independent mode-purpose models.
3 DATA PROCESSING
Data manipulation was undertaken with the goals of:
Defining trips according to mode and purpose
Identifying trips’ origin TAZs, destination TAZs, and durations
Estimating a trips’ generalized cost
Processing took place in order of the steps detailed below to most efficiently achieve these goals.
3.1 IDENTIFYING ORIGIN AND DESTINATION TAZ
First, using destination coordinates provided in the trip records, each record was matched to an origin and destination TAZ using TAZ geospatial data [provided by MAPC]. The destination TAZ was defined according to a record’s destination coordinates; the origin TAZ was defined according to the destination coordinates for the person’s previous record (i.e. the link just before the one of interest).
3.2 DEFINING TRIPS BY MODE
Modes of interest included non-motorized (NM), single-occupancy vehicle (SOV), high-occupancy vehicle (HOV), walk-access transit (WAT), and drive-access transit (DAT). For the NM, SOV, and HOV modes, trip records were used “as-is”: each record represented one trip. These three modes were defined according to the criteria in Table 1. For mode definitions, see Appendix Table A
| Trip | Classification |
|---|---|
| NM | Mode = 1 or 2, with any number of travellers |
| SOV | Mode = 3, 4, 11, 12, or 97, with one traveller |
| HOV | Mode = 3, 4, 11, 12, or 97, with two or more travellers; Mode = 8, 9, or 10 |
By contrast, trip records for WAT and DAT were chained together to create transit trips. Generally, a transit trip was defined as movement from location \(A\) to location \(B\), where all links between \(A\) and \(B\) were either on transit or, if not on transit, had a purpose of switching transportation for a subsequent transit link.
The following was considered a single WAT trip from home to work:
A person walks from their home to bus stop \(B1\)
They ride the bus from \(B1\) to bus stop \(B2\)
They walk from \(B2\) to train station \(T1\)
They ride the train from \(T1\) to train station \(T2\)
They walk from \(T2\) to their place of work
However, the following would be considered two transit trips: one WAT trip from home to the store, and one DAT trip from the store to work. This is two trips the case because the third step is neither on transit, nor involves switching to another transit link.
A person walks from their home to bus stop \(B1\)
They ride the bus from \(B1\) to bus stop \(B2\)
They walk from \(B2\) to the store, where they shop for groceries.
They walk from the store to train station \(T1\).
They ride the train from \(T1\) to train station \(T2\)
They walk from \(T2\) to their place of work.
After this chaining, these two modes were defined according to the criteria in Table 2.
| Trip | Classification |
|---|---|
| WAT | All links have Mode = 1, 2, 5, 6, or 7 |
| DAT | At least one link has Mode = 3, 4, 8, 9, 10, 11, 12, or 97 |
3.3 DEFINING TRIPS BY PURPOSE
After appropriate chaining, trip purposes were defined according to the criteria in Table 3. Purposes of interest included home-based work (HBW), home-based non-work (HBNW), and non-home based (NHB). For NM, SOV, and HOV trips, the destination purpose was the purpose for the record, and the origin purpose was the purpose for the chronologically previous record. For WAT and DAT trips, the destination purpose was the purpose for the last link, and the origin purpose was the purpose for the record chronologically previous to the first link.
| Trip purpose | Origin purpose | Destination purpose |
|---|---|---|
| HBW | 1, 2 | 3, 4, or 12 |
| HBNW | 1, 2 | Not 3, 4, or 12 |
| NHB | Not 1 or 2 | Not 1 or 2 |
3.4 DERIVING ORIGIN TAZ, DESTINATION TAZ, AND TRIP DURATION
After trips were fully defined, origin TAZs, destination TAZs, and trip durations were derived according to the criteria in Table 4. The calculation method differed based on whether the trips were single records (NM, SOV, HOV), or chained records (WAT, DAT)
| Trip | Origin TAZ | Destination TAZ | Trip durations |
|---|---|---|---|
| NM | Origin TAZ of record | Destination TAZ of record | Trip duration of record |
| SOV | |||
| HOV | |||
| WAT | Origin TAZ of first link | Destination TAZ of last link | Sum of trip durations for all links, plus sum of activity durations for all intermediate links |
| DAT |
3.5 JOINING TO SKIM DATA FOR GENERALIZED COST
The final step in data processing was joining the trip data to skim data [provided by MAPC]. This was a necessary step to obtain the generalized cost of a trip, which considers cost in terms of travel time, terminal time, waiting time (if transit), and financial cost. In modeling, generalized cost could be treated in a similar way to time: a single measure that could act as a sole determinant of decaying trip value.
Skim data was provided on a TAZ-to-TAZ basis, so was joined to the existing data according to origin and destination TAZ. Thus, measures of generalized cost were not specific to the trip, but rather generalized to the TAZ origin-destination pair.
4 MODELING METHODS
4.1 EXPONENTIAL REGRESSION
With one covariate, exponential regression takes the following mathematical form:
\[ log(d) = β_0 + β_1t \]
This can be re-expressed in the following way:
\[ d = αe^{β_1t}, \quad α = e^{β_0} \]
Where:
\(t\) is trip duration (or generalized cost)
\(d\) is the decay in value associated with \(t\)
\(\alpha\) is the expected decay in value when \(t = 0\) (\(e^{\beta_0}\) should \(\approx 1\))
\(\beta_1\) controls the rate of decay for the regression fit. (\(\beta_1 < 0\) always for decay models)
Regardless of the values of the regression parameters, an exponential decay function has a constantly increasing slope. This means that the function decreases most steeply at the beginning and gradually becomes flatter as \(t \rightarrow \infty\). Thus, in the travel time decay context, this model is most useful for the modes and purposes for which value drops off rather quickly.
4.2 LOGISTIC REGRESSION
With one covariate, logistic decay regression takes the following form:
\[ d = \frac{1}{1 + e^{−(β_0+β_1t)}} \]
This can be re-expressed in the following way:
\[ d = \frac{1}{1 + αe^{−β_1t}}, \quad α = e^{−β_0}\]
Where:
\(t\) is trip duration (or generalized cost)
\(d\) is the decay in value associated with \(t\)
\(\alpha\) and \(\beta_1\) together control the rate of decay for the regression fit. (\(\beta_1 < 0\) always for decay models)
Regardless of the values of the regression parameters, an logistic decay function has a constantly decreasing slope to an inflection point, after which it is increasing. This means that the function decays slowly at the beginning before a steep drop-off. Thus, in the travel time decay context, this model is most useful for the modes and purposes for which value stays relatively high until greater trip durations.
4.3 MODEL SELECTION
Modeling was completed for time for all mode-purpose pairs, and for generalized cost when available (all WAT and DAT models). To fit the models, the sample response at time (or cost) \(t\) was calculated as \(\scriptstyle d_t = \frac{|trips \, of \,duration/cost > t|}{|total \, trips|}\) – in other words, the proportion of trips going longer or costing more than \(t\). Functional form for the model – exponential or logistic decay – was determined at the discretion of the analyst by plotting \(t\) against \(\hat{d_t}\) and observing the shape of the data. The plots for trip duration models are shown in Figure 1. The plots for generalized cost models are shown in Figure 2.
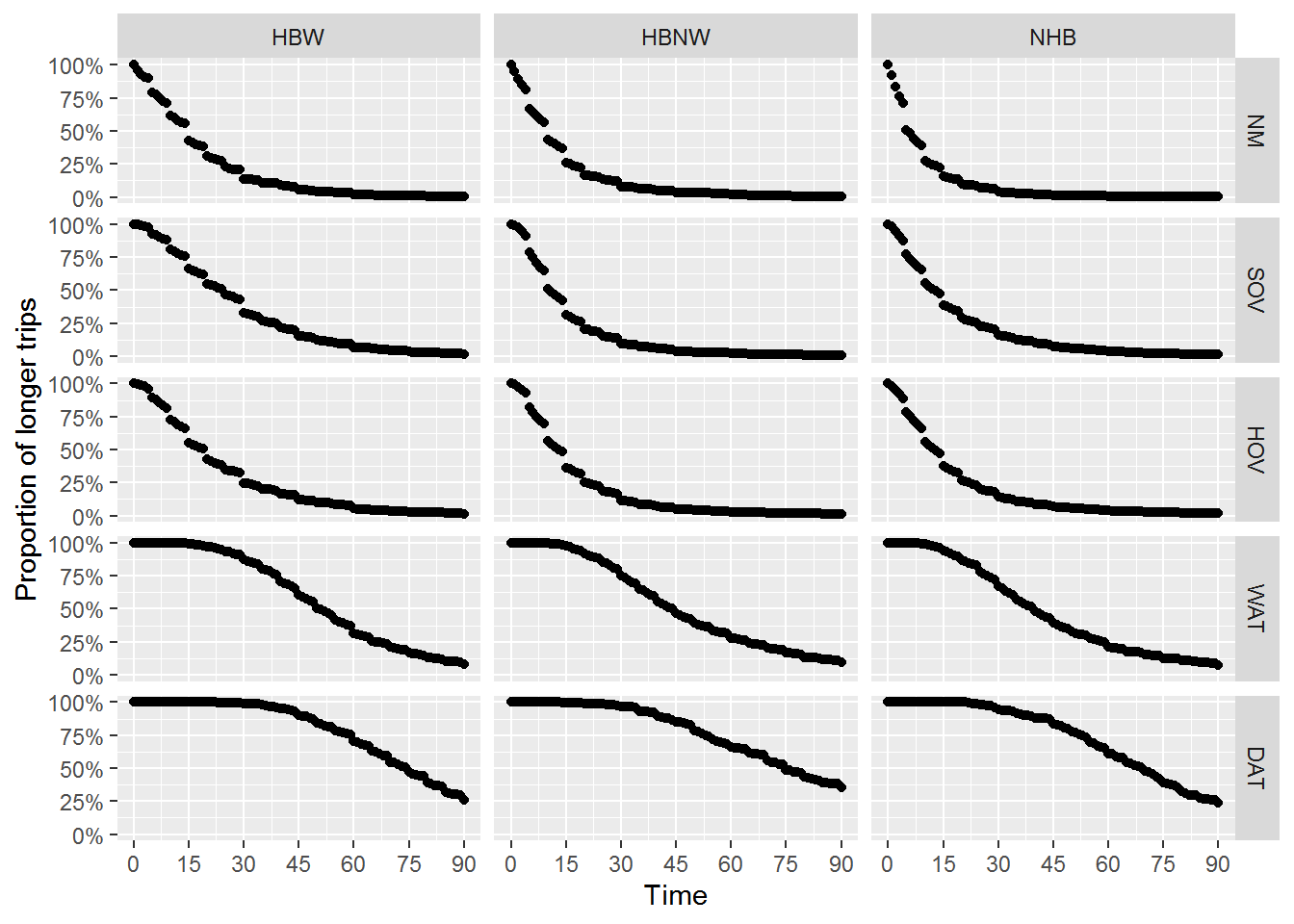
Figure 1: Data form for trip duration models
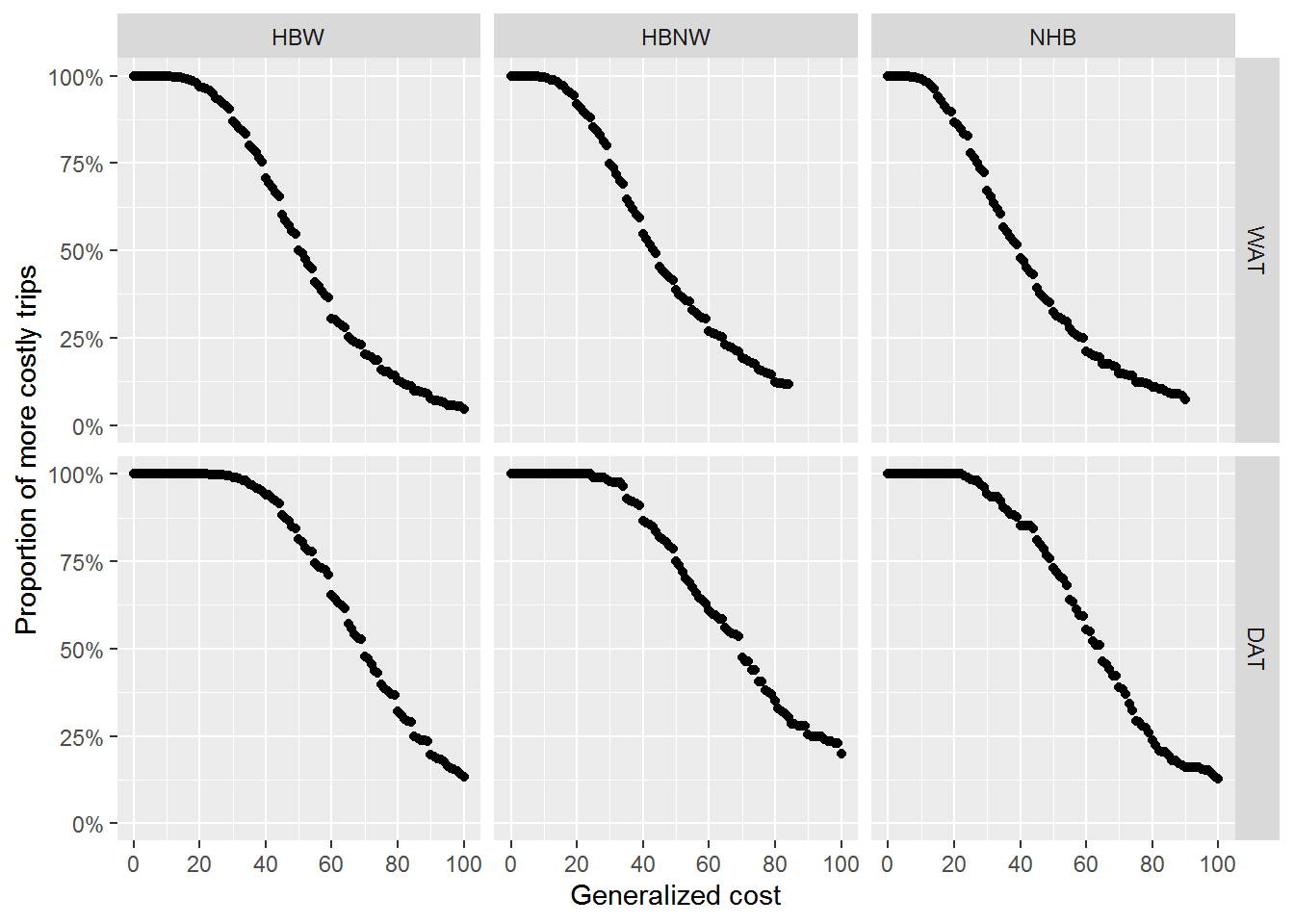
Figure 2: Data form for generalized cost models
For the trip duration models, exponential decay was selected for all purposes for NM, SOV, and HOV modes; logistic decay was selected for all purposes for WAT and DAT modes. For the generalized cost models, logistic decay was selected for all models.
Because of some unusually high-valued trip times and generalized costs, all models were built on the set of values of \(t\) in a mode-purpose pair for which \(\hat{d_t} \geq 0.1\). This prevented the models from overfitting the right tail, which consisted of very low-probability, unlikely trips. Though this constrained the modeling set, it provided a more practical model by fitting to more common trips.
5 RESULTS
The model results are provided in Table 5, and resulting equations are provided in Table 6. The high \(R^2\) and low \(AIC\) values (for exponential and logistic decay, respectively) indicate that, over the constrained modeling sets, the fits perform quite well. Though using these models to predict very long or costly trips would be extrapolation because of the constraints on the modeling sets, these need for these types of predictions is minimal given the time and generalized cost for most trips.
| Trip | Measure | Purpose | \({\beta_0}\) | \({\beta_1}\) | \({R^2}\) | \({AIC}\) |
|---|---|---|---|---|---|---|
| NM | Time | HBW | 0.145 | -0.064 | 0.986 | NA |
| NM | Time | HBNW | 0.033 | -0.081 | 0.982 | NA |
| NM | Time | NHB | 0.004 | -0.114 | 0.983 | NA |
| HOV | Time | HBW | 0.154 | -0.048 | 0.993 | NA |
| HOV | Time | HBNW | 0.167 | -0.073 | 0.989 | NA |
| HOV | Time | NHB | 0.085 | -0.065 | 0.994 | NA |
| SOV | Time | HBW | 0.248 | -0.044 | 0.982 | NA |
| SOV | Time | HBNW | 0.138 | -0.078 | 0.986 | NA |
| SOV | Time | NHB | 0.037 | -0.059 | 0.995 | NA |
| WAT | Time | HBW | 4.581 | -0.085 | NA | 41.835 |
| WAT | Time | HBNW | 3.500 | -0.072 | NA | 48.898 |
| WAT | Time | NHB | 3.304 | -0.076 | NA | 46.802 |
| WAT | Generalized cost | HBW | 4.048 | -0.201 | NA | 20.174 |
| WAT | Generalized cost | HBNW | 3.977 | -0.239 | NA | 17.414 |
| WAT | Generalized cost | NHB | 3.791 | -0.253 | NA | 17.027 |
| DAT | Time | HBW | 5.507 | -0.072 | NA | 48.313 |
| DAT | Time | HBNW | 3.241 | -0.037 | NA | 93.461 |
| DAT | Time | NHB | 4.503 | -0.062 | NA | 55.387 |
| DAT | Generalized cost | HBW | 3.831 | -0.113 | NA | 33.326 |
| DAT | Generalized cost | HBNW | 3.511 | -0.118 | NA | 31.402 |
| DAT | Generalized cost | NHB | 3.122 | -0.102 | NA | 37.257 |